概率论是每个数据挖掘人员必修的课程,特别是对算法的理解程度,很大程度上取决于自己的功底扎实不扎实。这里,我给大家总结了一些常用的概念及其推导,包括总体和样本的关系,均值、方差、标准差、协方差等。
总体均值(期望):表示总体的平均特征。
![]()
总体方差(方差):表示总体的偏离程度。
![]()
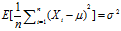
(1)
样本均值:表示样本的平均特征,是总体均值的无偏估计。
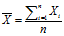
样本均值的期望
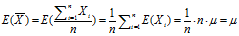
由上式可知,样本均值![]() 是总体均值
是总体均值![]() 的无偏估计。
的无偏估计。
样本均值的方差
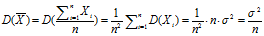
样本方差:表示样本的偏离程度,是总体方差的无偏估计。
自由度(自由取值的个数)为![]() ,因为计算样本方差之前需要把样本均值计算出来,那么自由取值的个数为
,因为计算样本方差之前需要把样本均值计算出来,那么自由取值的个数为![]() 。
。
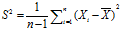
样本方差的期望
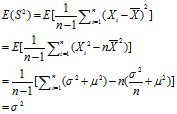
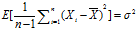
(2)
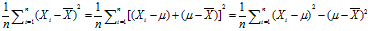

(3)
当![]() 时,
时,
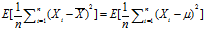
(4)
无偏估计和有偏估计:
由公式(1)和(2)可知,
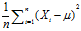 和
和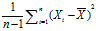 是总体方差
是总体方差![]() 的无偏估计,
的无偏估计,
由公式(1)和(3)可知,
 ,即
,即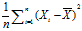 是总体方差
是总体方差![]() 的有偏估计,低估了总体方差
的有偏估计,低估了总体方差![]() 。
。
由公式(1)和(4)可知,
当![]() 时,
时,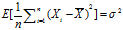 ,此时
,此时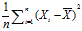 是总体方差
是总体方差![]() 的无偏估计。
的无偏估计。
样本标准差:
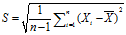
样本协方差:表示两个样本参数之间的相似度。
协方差的结果是先求“参数x”与“参数x的均值“之间的之间的差,以及“参数y”和“参数y的均值“之间的差,表达了两个参数xy之间的差异程度。
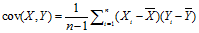
协方差矩阵:
若观测的一个系统有3个参数xyz,而协方差只能计算两个参数之间的差异程度,可以用协方差矩阵来表达参数两两之间的差异程度。
协方差矩阵是一个对称的矩阵,而且对角线是各个维度的方差。
为了给大家提供更好的体验,现输出两张图片格式的总结,供大家学习下载:
转载请注明:宁哥的小站 » 概率论基础之均值方差协方差